A Theory Of Nothingness: M0

In the beginning there was nothing and everything at the same time. (anon)

M0=,/,
SM0=0!/0^0={1/1,1/0}
0^0 is double valued, {0,1}. A special case of x^y. From x it looks like 0, from y like 1. We are forced to consider two variables {x,y} since exponential is hierarchical. exp(y*ln(x)) is the dual of x^y, reflecting the duality 0^0={0,1}. M0 has either 1 state or infinite states at the same time. If you want fireworks it seems you gotta measure zero.

The duality of measurement (or counting) is exposed here. Combinatorial for given exponential. Measurement is relative to a base which is the normal case. The norm is exponential in the universe. Everything is expressed as compared to a base which is always quantised. 0^0 expression is attempting to take 0 as base and this creates problem. This will be resolved by transforming to M0+ and taking a boolean base, 2^0. The nominator is factorial since it measures complexity of the meta structure on top of base.

A state is needed to express just a point. But this state is only needed in retrospect to M0+=E0/H0 to explain H0={}. M0 reflects the identity element. In fact (,/,) reflects the concept of nothingness better. Something really insignificant compared to itself. Then Higgs is M0 since (,/,) looks more like a self interacting scalar or dust field. No dimensions and infinite dimensions live together here. A bit like the impulse function, or rather Dirac Delta Function;

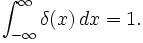
Like we had to consider x^y form when looking at 0^0, here we have a duality, {position, intensity}. In fact Delta Function is the algebraic definition of a point;

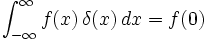
It can be defined in any space, the simplest being one dimensional.

Although it looks thorny, it is possible to deal with it analytically and an essential part of dynamical system analysis. In electrical process control, a system is defined by it's impulse response. It seems ATON has landed on it's analytical bottom. This is the place to dwell for a while and maybe look at some quantum mechanics.

There is also the discrete equivalent of DF, Kronecker Delta Function with similar properties to DF;