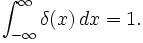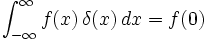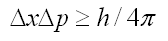


The uncertainty principle (by Heisenberg) is expressed by a dual duality in physics,
D={{P,M},{T,E}} = {{Position,Momentum},{Time,Energy}}
It states that the uncertainty in the measurement of "coupled" entities is always larger than a cetain limit, Planck's constant divided by 4pi. Momentum is also a function of position, and energy is also a function of time.
It is a statement of prediction. It predicts that nothing can be measured beyond a certain limit, with the available means of D. It applies to every measurement process, therefore to everything. For example, measurement of pitch in sound is optimised by balancing accuracy (the length of the buffer (window)) with timeliness. Speech recognition and synthesis is an event that has to happen in real time. Therefore parameters like pitch are measured in flight. Longer windows give more accurate measurement of pitch, but the location is lost. Shorter window locates the pitch better but misses length for accuracy of intensity. Therefore an optimum buffer length is used.
Note the black hole form in the action divided onto a spherical surface. 4pi is the amount of solid angle around a point in 3D space.
Since it is a statement of prediction, it suits quantum mechanical language well. QM's language is probability. It has an involved derivation but I will go through it, since it is so important...
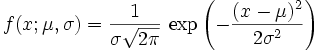













 What do you reckon?
What do you reckon?