Complex Normal Distribution

I called it CND but I haven't seen it defined. I just put complex variables in ND;

z=(1/c1*sqrt(2*pi))*e^((-1/2)*((z-c0)/c1)^2)





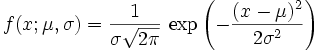
Where c1 and c0 are standard variation and mean. In the following c1 is the free parameter. A surprise here is that Mandel and Julia are similar in large scale. Although ND has that property of looking similar after a frequency transformation.

As before, restricting expansion also limits domain. I think I made a mistake with the expansion of CND. Fractal Explorer's Exp(z) does not give Taylor's expansion to a number. The expansion is not so trivial to calculate. Too many terms. I will keep the "expanded to 6" ones until I correct them. Currently I am trying to learn some Java.

Mandel
e^x expanded to 6
Sitting Buddha, hmm
















Julia
e^x expanded to 6
c1=(1.01,-1.11)
Doesn't it look like infinity sign?
Unfortunately the above Mandel
is not at the same c1, Mandel is below









Mandel
e^x to 6












Mandel
bailout=49













Mandel
bailout=324











Julia
bailout= 25












Mandel
bailout=25












Julia
bailout= 361












Mandel
bailout=361












Mandel
c0 free












Mandel
c0=(0,-1)
e^x expanded to 6
Mandel as mouth